Spirits and the incompleteness of physics
Complexity, renormalization, and the spirits beyond the horizon of theory
In 1953, Richard Feynman ended a conference talk in Kyoto with an apology. The famous physicist seemed embarrassed—he'd left part of his problem unsolved. Feynman had been presenting on helium's superfluid phase, but phase transitions were new territory for him. After the talk however, the famously terse Nobel laureate Lars Onsager shared with the audience that
Mr. Feynman is new in our field, and there is evidently something he doesn't know about it, and we ought to educate him. So I think we should tell him that the exact behavior of the thermodynamic functions near a transition is not yet adequately understood for any real transition in any substance whatever. Therefore, the fact that he cannot do it for He II is no reflection at all on the value of his contribution to understand the rest of the phenomena.
This was the state of affairs in the fifties. We'd figured out quantum mechanics and relativity, yet something so mundane as boiling water1 was stumping the great physicists of the time. That is, so it was before Ken Wilson ushered in his revolution.
Wilson's ideas from the sixties and seventies—effective field theory and the renormalization group—rank among physics' deepest discoveries. They started as tools for understanding phase transitions but ended up revolutionizing how we think about the laws of nature. Few concepts from my physics career have shaped my thinking more broadly than these. Yet I'd wager most non-scientists have never heard of them. This makes sense given their dull names, but don't let that fool you. These ideas deserve to sit alongside quantum mechanics and relativity. I'll argue they're just as weird too. In fact, using these ideas together with concepts from computational complexity, I'll make the case that the universe plausibly contains phenomena worthy of the name spirits.2
I. Renormalization and hints of incompleteness
Physics is supposed to be the fundamental science. The standard story goes like this: given the laws of physics plus infinite computing power, we can predict any phenomenon in the universe. Sure, we don't understand dark matter or black hole interiors yet, but that's just because we haven't found the right laws. Once we do, it's game over. Everything reduces to simple laws whose consequences can be deduced with infinite compute. This picture might be completely wrong, however.
First, Gödel's incompleteness theorems say that this does not logically follow. There could be consequences of the laws of physics that are unprovable through any computation whatsoever. Erik Hoel had a wonderful post last year about the possible ramifications of Gödel incompleteness for science and consciousness that I highly recommend.
So non-trivial implications of Gödel incompleteness for physics is very much a live option. As Erik points out, research has uncovered a toy model quantum system that suffers incompleteness, making it impossible to determine the so-called spectral gap: the energy difference between the two states of lowest energy. That said, this model is quite different from our best theories of fundamental physics and relies heavily on the toy system being infinite in a very particular way. And infinity is truly at the heart of Gödel incompleteness. So it's unknown how much of a restriction Gödel places on our physics.
However, here I want to point out other severe dangers for physics that do not rely on Gödel at all.
To understand these dangers, we first need to see how modern physicists think about the laws of nature. The key concept here is scale. When you hear "scale", you probably think of size. But a soccer ball and tennis ball aren't really on different scales—their sizes are too similar. What matters are dramatic differences of size.
So what counts as being of different scales? The key concept is resolution. To understand any phenomenon, it is of utmost importance that you set your resolution correctly. Change the scale, and you'd better adjust your resolution or you're dead. Too coarse, and the information you need disappears. Too fine, and your phenomenon drowns in irrelevant details.
You might think irrelevant details are better than missing information. But for practical purposes, they're equally useless. Your computational limits ensure the information you need is completely inaccessible—it might as well not exist. It's like using the standard model of particle physics to describe a cannonball's trajectory. Sure, maybe with a Dyson sphere powering your supercomputer you could do it. But if you value your sun, it's a stupid idea.
But wait—how sure are we that even a Dyson sphere would work? I've been saying too fine resolution is bad "only for practical purposes", and this caveat is essential if you believe everything reduces to physics. But I'm much less confident in "only for practical purposes" than I used to be. In fact, I'll soon argue the problem isn't just practical.
But I'm getting ahead of myself. What we've implied above is that different scales require different instruments—of measurement, of language, and of mathematics. The theory best suited for prediction throws out the maximal amount of irrelevant information while keeping as much information pertinent to your phenomenon of interest as possible. A very delicate balance.
We call theories designed for the right scale effective field theories (EFTs). These have been wildly successful in modern physics. I could list their achievements, but in reality, almost all successful physical theories are now understood to be EFTs. Even our supposed fundamental theories like general relativity or the standard model of particle physics.
So how do you build an EFT? You write down the most general theory consistent with a few basic principles: what you want to predict, the symmetries of your problem, plus whatever axioms you won't compromise on—usually quantum mechanics and relativity, and at the very least locality. This leaves a handful of free parameters you can't predict from first principles. You just have to measure them.
A mind-boggling fact, however, is that such theories exist for any physical phenomenon at all. How on earth can we write down predictive theories that depend on just a handful of parameters? This is basically asking: how can we predict a cannonball's trajectory knowing only a tiny amount of information? The cannonball consists of an enormous number of atomic subcomponents, each one an independent knob that can be dialed to adjust the state of the cannonball. Why don't these many unknown pieces of information, far exceeding what's captured by the ball's mass, add up to a giant blob of unknowability?
Somehow, all that fine-grained information gets compressed into just a few numbers that characterize your system's behavior. For the cannonball, just the mass. How does this compression happen? Why aren't there 34 different constants we need to measure to predict the cannonball's trajectory? Don't think this is obvious—it's not. We're just used to it.
Yet, no one has managed to write an "EFT of human history". But humans are basically giant blobs of erratic atoms interacting with each other. Why does physicists get nice simple theories while historians gets chaos?
To understand when EFTs work, we need the second star of the show: the renormalization group. This is the technique that shows how tiny-scale physics gets compressed into just a few numbers that affect larger scales. The key ingredients enabling the miracle are locality (no action at a distance) plus relativity (no preferred reference frames).
Fortunately, we can understand the main insights through a simple little example that lets us skip the mathematical heavy lifting that shows generality of the mechanism—you should consult this absolute beauty of a paper by Joe Polchinski for that.
Here's the example. Consider a frosted glass panel:
Shine a beam of light on it at an angle. Some light transmits through, some reflects off. We'll focus on the reflected light.
Say you're hoping for a theory of the reflection angle without worrying about all the microscopic details inside the glass. If the glass were perfectly smooth, this would be trivial—the incoming angle equals the outgoing angle:
Makes sense:
With low-energy photons, the simple formula still works approximately, even if the glass isn't perfectly smooth. Here's why. A basic physics fact is that photon energy is inversely proportional to wavelength:
So low-energy photons have long wavelengths and "wiggle" over longer distances.
The picture tries to show why this matters. A long-wavelength beam can't "see" tiny surface imperfections—they're too small compared to the wavelength. They average out. But a high-energy green laser has tiny wavelengths, so it suddenly becomes sensitive to, even dominated by, little bumps and scratches.
The imperfections have their own characteristic typical size, call it L_pane. Once you account for this, your scattering formula becomes:
The g_i's are different numbers that characterize the pane's imperfections. The series is infinite—higher and higher powers of energy appear, with an infinite number of constants. These g_i's are completely non-universal. They depend on arbitrary microscopic bumps and scratches at the exact spot where your beam reflects. Move your laser to a slightly different location, and you'll have to remeasure g1, g2, g3... all the way up to g42 and beyond.
An absolute nightmare.
Thankfully, the effects of this disaster is usually not felt. If the photon energy is low enough, then:
Let’s say this product equals 0.01.3 Then:
You can ignore all the g_i's and barely make any error. This assumes the g_i's aren't gigantic, but wonderfully enough, Polchinski's absolutely hottie of a paper show they're typically order unity. So microscopic details affect the reflection angle, but negligibly at low energies. Phew.
This isn't just a quirk of glass panels. The renormalization group shows that relativity plus locality almost always guarantees this same pattern:
By "simple" I mean something that depends on just a few constants, independent of whatever mess happens at short distances.
Now, studying low-energy physics is basically the same as studying large-scale physics. So the renormalization group tells us why we can ignore tons of microscopic information—like atomic jiggling inside a cannonball. But two conditions must hold: (i) you're not trying to predict high-energy phenomena, and (ii) you're willing to accept limited precision.
Push too far into the decimal places, and all kinds of microscopic junk starts influencing your answer. But those first few digits? Locality and relativity are the bodyguards keeping the microscopic madness at bay.
Now, if you want to go to high energies, you are in trouble. Consider making your photon purple, so it has a lot of energy, say E L_pane = 4. Then we get
Ouch. The sum blows up to infinity, and your theory is obvious nonsense in this regime. Now you must cook up a new theory integrating the detailed dynamics of pane itself. You have no choice but to model a bunch of stuff that you previously had the luxury of ignoring. This sounds like work, but's such is life.
So you do the hard work of modeling new details to understand light-pane interactions. You discover new patterns, leading to the quantum theory of atoms. This eliminates your old problematic series expansion—wonderful! Your new theory might predict some complicated formula for the outgoing angle, but it's no longer a series in E×L_pane, so no more nonsensical infinities.
But a new infinity lurks around the corner.
A new, smaller scale
has just appeared. Your improved theory gets corrected by a different series expansion, caused by this new characteristic length. This scale represents the new boundary below which you've ignored some physics. Sure, it's smaller than before, so you can push to higher energies. But go even higher, and you need to work even harder. If you do that, you discover quantum electrodynamics—the proper relativistic theory of electrons and photons.
But QED also breaks down at high energies. It has its own breakdown scale. So you assemble an international team, build a particle accelerator, and discover the standard model of particle physics. You might think that it stops there, but no, it doesn’t. We know very well that our understanding of gravity breaks down when energies gets close to the so-called Planck energy.
Every theory we've found breaks down at high enough energy. This is well understood and doesn't necessarily spell doom for physics. But there's another frontier where theories break down—one that's less appreciated and that signals real trouble.
II. The complexity frontier
Take a box with a few hundred atoms at low temperature, perfectly isolated from the environment. Low temperature means we're in the regime of understood physics. Imagine we can measure every atom's position and velocity precisely.4 We leave the box alone for a long time, then ask: where are all the atoms now?
With unlimited computing power, our best theories should handle this easily. But they can't. There's a finite time horizon beyond which no physical theory in our possession can predict the atoms' locations—even at low energies, and even with a galaxy of Dyson spheres powering our GPUs.
To see why, let's set up a cartoon picture that captures the essential effect.5
Focus on one atom. Our little guy travels in a straight line until he bumps into another atom. His direction and velocity change, then he travels in a new straight line until the next bump. This repeats endlessly. Seems fine—we can compute the angle and velocity changes, so we should be able to track all collisions. Our Dyson galaxy of computers can handle it.
But every collision introduces a tiny error. Being maximally conservative, pretending no new physics occurs before the Planck scale, our calculation drifts from reality by roughly:
where ℓ_Planck is the Planck length—the scale where quantum gravity matters. This error lives extremely far out in the decimal places. The Planck length is absurdly tiny.
But errors accumulate. As time passes, your estimates of atomic positions and velocities drift from whatever nature is actually doing. We have no theory to account for these errors. Eventually, you lose track of when and where collisions happen. Your predictions become worthless.
The answer to "where is this atom later?" becomes completely unanswerable, even with unlimited computing power.
Your sin was asking a question that requires too many queries to our theory of physics before producing the final answer. This mechanism is completely general—all our theories break down at high complexity.
There's an obvious attempted fix though: first go ahead solve quantum gravity with those gigantic computers, thus eliminating the errors in your theoretical predictions. But this assumes something that could be totally wrong. Namely, it assumes that our search for an ultimate theory eventually terminates. This belief is despite most empirical evidence. Every time we've zoomed in on nature, we've discovered new stuff. How do we know there will ever stop being new details as we keep zooming? How do we know the laws of physics aren't fractal-like?
I'll argue we're in trouble even if they're not fractal-like all the way down. But let's assume they are for now.
If new physics keeps appearing as we zoom in, we'll never have an ultimate theory. Instead, every theory will have finite precision and a finite predictive horizon, even in principle. You might hope that as theories improve, the horizon of the explainable expands in all directions. But even that's questionable.
Assume I have a fixed compute budget. Finding a "better" theory—one valid at shorter distances—might not help much at all. The problem is that "more fundamental" theories are always more computationally expensive. Just ask my friends trying to simulate a handful of quarks on supercomputers—a physical system with total mass roughly 10^{-30} times your bodyweight.6
So as you improve your theory, there are directions in phenomenon-space where you don't push your horizon forward with a fixed compute budget. The only way to hope to explain all phenomena is if your compute budget grows alongside your discovery of new theories. But this hope is dangerous.
Two limits together put an upper bound on the compute you can ever use. First, the universe expands at an accelerated pace, creating a so-called cosmological horizon. The implication of this is that only a finite volume of the universe is accessible to us. Second, our best hint about quantum gravity—the Bekenstein-Hawking entropy formula7—suggests that finite volumes of space contain finite amounts of information. So evidence supports there being a finite amount of compute available to us, bounding the horizon of explainable phenomena.
This finite compute creates trouble even if there is a final, error-free theory of physics. Even with a perfect theory, we can't work out arbitrary consequences. While each individual "query" to the theory is error-free, we only have a finite number of queries at our disposal. Only so many atomic collisions we can predict.
Now, hearing "finite information," you might get excited. How can that not be knowable in principle? In a trivial way it is—our patch of the universe describes itself, I guess. But acknowledging this doesn't amount to having a theory of it. It's like saying a map of the world at 1:1 scale is technically complete. Sure, but good luck folding it.
To possess a theory is to possess a compressed representation of information that grants predictive power. The finite information content suggested by the Bekenstein-Hawking entropy quantifies how many measurements you'd need to completely determine the initial conditions in our patch of the universe. This also represents the "storage capacity" of our part of the universe.
Now comes a remarkable calculation we can make. I don't assume you're a physicist, so I'll just describe the result—see footnote for the full computation.8 If our patch of the universe is (1) described by finite (but possibly gigantic) information, and (2) we believe quantum mechanics, then we can show this:
In the worst case scenario, it's impossible to store the laws of physics inside the universe itself!
The derivation uses a few technical terms, but the idea is remarkably simple. In quantum mechanics, the laws of physics are completely captured by a single matrix—a rectangular array of numbers known as the Hamiltonian.9 This array uniquely defines an action on matter in the universe, corresponding to evolving time forward. Under the assumptions of quantum mechanics and finite information, the matter in the universe is equivalent to a collection of so-called quantum bits—qubits. But the information required to uniquely specify this matrix is much larger than the information storable in the qubits:
So the laws of physics might be described by more numbers than you can store in the visible universe. Mind-blowing, if you ask me. And you can't necessarily solve this by positing a larger "hard-drive universe," because the same complaint applies to that universe too.10
I can already hear former colleagues' complaints about suggesting that this possibility might be realized. The known laws are simple! The observed laws have so many symmetries!
All well and true. It's certainly possible that the exact, error-free description of the laws is short enough to be stored within our patch of the universe. This would work for a highly symmetric Hamiltonian matrix where most elements are zero, perhaps something like this:
Most elements being zero is a consequence of locality, it turns out, while the equality of various elements represents the independence of physics of location. But I'd like to point out that we've actually studied only an absolutely tiny fraction of the total information in the universe. In matrix language, we've really investigated only a tiny fraction of the numbers in this matrix. Like, I mean, really really tiny.
According to this paper, the information stored in matter we understand reasonably well is roughly 10^89 bits, while the information in our patch of the universe is 10^122 bits. That is, the matter we think we understand decently represents a fraction:
10^{-33} = 0.000000000000000000000000000000001%
of the information content. Who knows, maybe this absolutely tiny subset of matter is described by particularly nice and tidy laws? There are good reasons to think so.
A much larger fraction of the observable universe's entropy is carried by supermassive black holes. This is about a quadrillion times larger than the amount of standard matter (but it’s still an absolutely tiny fraction—most resides in the unknown). Modern research on the holographic nature of quantum gravity suggests that black holes are intimately tied to chaos and the butterfly effect (classic paper). And there are very good reasons to believe that spacetime and thus locality becomes completely corrupted inside a black hole—good old Einstein's general relativity predicts this. This hints that you're reaching whole new levels of complexity, associated with the breakdown of locality. And locality is what made your laws so nice and tidy in the first place. But let’s say that physicists ramped up their experiments to measure about a (quadrillion)² times more stuff than what we have seen in the universe so far. Even then, if we kept finding locality, the best we’d get is an array of numbers encoding the laws of physics that still looks like this:
where the unknown might be highly irregular and dense. But at present, that green box represents a fraction of 10^{-33} of the rows and columns, and only there do we know that the matrix is sparse, i.e. locality holds.11
In fact, albeit working with a toy model of quantum gravity, my collaborators and I published results last year hinting that black holes might be a mechanism that "hides" exponentially complex aspects of the laws of physics. It must be said that this is speculative work, but it fits with the picture that is emerging in modern theoretical work on black holes.
So, we often assume all of physics is local because the tiny sliver of the universe we engage with appears to be local. But we can make a reasonable anthropic argument for why, even if the universe fundamentally lacks locality, humans would arise as dynamical phenomena instantiated on degrees of freedom whose dynamics look local. Humans are patterns that somehow persist and replicate with high fidelity, and non-local chaotic dynamics might be too unstable to allow anything like this. In fact, spacetime itself may be viewed as the optimal "compact description" of this sector of relatively simple physics. So if we were to exist, we almost certainly would exist in a nice tidy corner of the matrix.
III. Spirits
Now we are in a weird situation. The laws of physics that we are able to write down in our universe, even in principle, might be incomplete, and so they are fundamentally limited in their predictive power. What does that mean, pragmatically speaking? It means that as we go out in nature and observe patterns of sufficient complexity, there might be no way for us to (1) explain how they got there and (2) explain how they will evolve.
There are strange consequences implied by this picture. We can now imagine that there are two distinct theories out there that describe different phenomena seen in nature, one of them being what we traditionally call physics. Yet, the two theories might be computationally inaccessible from each other. Physics cannot derive the other theory even given access to all compute in the universe, and vice versa. And so, what does it mean to say that physics is more fundamental? Not much, in fact. You can say that physics is a mind-blowingly good theory—better than any other humanly known scientific theory at present. But not fundamental, if this is the state of affairs.
You might say that in some hypothetical Platonic realm with infinite computing power, you can derive the other theory from physics. But I'm skeptical of such sleights of hand. An deep lesson from physics is that information must be instantiated on physical resources.12 In fact, heat is nothing but information you lost track of. Seriously, I'm not being facetious here. That is literally what heat is. There's even a phenomenon called reversible computing where, if you never discard any information, you produce no heat. Zero. Nada. Insert Carnot's shocked face here.
So, saying there is a Platonic realm where we can connect all other theories to physics, implying that such a thing "exists", is possibly as meaningful as saying "blarb is glarb". Both statements have equal implications, in pragmatic terms, for our possible experiences of the universe.
Of course, these other theories, if they exist, are probably much more complex than physics. There's a reason we (probably) haven't found them yet. Either way, we might have this situation:
But what about the no-man's land in between theories? What on earth is that?
Let's be sure we read the picture correctly. What I'm implying is that there's no theory for the natural phenomena living in this region. But what does that mean? What is a theory, even?
A theory is nothing more than a compression of observed patterns. Physics is great because it's so damn good at compression. We observe all these seemingly disparate, highly complex phenomena that all seem unique. But physics realizes they're actually characterized by a surprisingly small amount of irreducible information that can be decompressed using the laws of physics.
The statement that physics is fundamental becomes the claim that physics can compress any observed phenomenon that any other theory can compress—although physics might be much less efficient at decompression/compression than a more specialized theory.
You might be perplexed here, since we usually say that what makes a good theory is that it can predict or explain. But prediction is really just a roundabout way of checking if you have a correct compression scheme for the class of phenomena you're observing. When you can compress, you have isolated what information is irreducible and what is redundant, and you can reproduce the redundant information from the irreducible information.
But you can easily fool yourself by building a seeming compression scheme that works on a few instances of your phenomenon, but the danger is that you've overfitted to these and basically just hardcoded their patterns. The way to check that you haven't is to predict.13
So to say that a phenomenon cannot be described by a theory is to say that there is no significant compression of it. These are dynamical phenomena taking place in the universe whose only accessible description is just themselves. There is no shorter description of the phenomenon than just recording it.
But there is nothing that rules out such phenomena actually having causal contact with our lives. Phenomena that influences our life trajectory, but which cannot be theorized over. Forces in the universe that can only be observed in their singular appearances, never captured nor even capturable by theory. I cannot think of a phenomenon more worthy of the name Spirit.
If you liked this post, you might like some of my other works:
God is NaN
The other day, a liberating thought fell into my head. I can reject naturalism and the supernatural at the same time, for the simple reason that the dichotomy is devoid of meaning. Refusing it seems to be the only sensible thing to do. And, as it turns out, the world regains a whole lot of color upon discarding the false sense of closure provided by nat…
My favorite Norwegian painter
Every time I visit my hometown in Norway, I go on a little excursion to Sigstadskogen. My destination is a small cluster of houses in a forest clearing, ten minutes’ walk from my mother’s home. One of the buildings that greets you is this:
We are really talking about so-called continuous phase transitions here. This only applies to boiling water if we also have the pressure set exactly correctly, so I am really talking about boiling water at that pressure. Another example of a continuous phase transition happens when a ferromagnet heats up and suddenly looses its magnetism.
Good thing I'm no longer pursuing tenure as a physicist.
Like any gentleman of sophistication, I’m using natural units, where the speed of light and Planck’s constant are equal to unity.
Also, Wikipedia was clearly not written by a gentleman, because it is wrong when it says “While natural unit systems simplify the form of each equation, it is still necessary to keep track of the non-collapsed dimensions of each quantity or expression in order to reinsert physical constants (such dimensions uniquely determine the full formula).” Why is it necessary? It’s only necessary if you want to convert back to a different unit system for plebeians, which is not forced on you—it is pure convention to say that we are measuring time in second rather than meters, etc. You can live all your life in natural units, which is the most gigachad thing I have ever heard of.
Of course, quantum mechanics forbids this, but the example doesn’t really rely on precise measurements, or that you measure positions and velocities in particular. It is just chosen for ease of presentation. Also, see the footnote below.
The more robust way of framing thing is to say that if you compute an N-point local correlation function, once N becomes extremely large, your theoretical predictions become complete nonsense.
Also as mentioned above, we shouldn’t really talk about positions and velocities, as these are problematic terms in quantum mechanics. But the point stands, these are irrelevant simplifications for our argument.
You might wonder: how on earth does this count as high energy? The point is that the energy densities involved in the phenomena under study are extremely high still.
In this case we should perhaps really say the Gibbons–Hawking entropy formula, since we are talking about a cosmological horizon rather than a black hole event horizon.
Consider a Hilbert space of dimension 2^N, ie described by N qubits. We can always represent a finite quantum system in terms of qubits (or similar objects). Now, the law’s of physics in quantum mechanics are described by the Hamiltonian—the time-evolution operator. Now if you want to store the laws of physics themselves in the qubits in such a way that they can be uniquely discriminated from other laws, there needs to exist a map from the space of Hamiltonians to the space of N-qubit quantum states. H→|H>. Distinguishability requires that we must be able to find states such that for any two different Hamiltonians H and H’ their corresponding quantum states are orthogonal. But this is impossible! Orthogonality means we need a basis that counts all Hamiltonians. But the space of Hamiltonians is continuous, while the number of basis elements is finite (2^N in number)!
Only a bit over a half of these numbers are independent since the matrix is Hermitian:
There are complicated things to be said here about the Wheeler deWitt equation and the fact that the GR Hamiltonian is a boundary term (and so it might be zero, if we are in a closed universe). But focusing on the visible universe, which has a boundary, lets us avoid this discussio.
Strictly speaking, we also know that the off-diagonal “thin bands” below and next to the green box must be sufficiently small.
But there is something weird going on here though. Where is the info of the Hamiltonian instantiated? Is you pull on this thread so seem to be heading in the direction of Platonism, I can’t deny that.








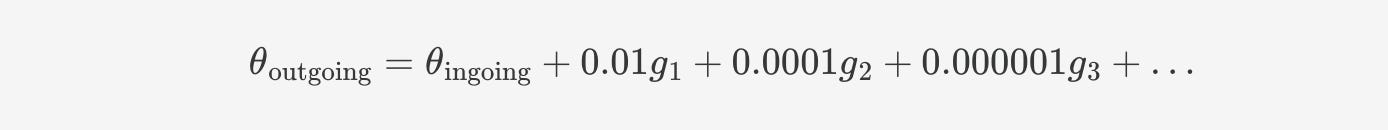






Great read even if I did not get all the math. This reminded me of Bernardo Kastrup saying that the universe cannot compute its next outputs even though they are deterministic and thus experiencing is the best way to know what happens next (I’m paraphrasing from memory so I apologize if I am not being precise). I would love to know your perspective on free will based on your background.
I'm confused as to how it could both be the case that, 1) as we zoom in on nature, more details reveal themselves and this could potentially go on forever, AND ALSO 2) there is finite information in finite space.
Is more detail at smaller and smaller scales not more information?